
Il y a sondage et sondage…
Pour mener leurs enquêtes, les statisticiens publics procèdent par sondage. Mais leur pratique est bien différente de celle des très nombreuses enquêtes publiées quotidiennement, lesquelles interrogent en général de l’ordre du millier de personnes, sans toujours se soucier de la représentativité de ces personnes. Faute de disposer d’une connaissance complète de la composition de la population française, les personnes interrogées dans ces enquêtes sont, dans le meilleur des cas, sélectionnées selon la méthode des quotas (par sexe, âge, profession, etc.). Les sondages de la statistique publique peuvent en revanche s’appuyer sur la connaissance de la composition de cette population. Dès lors, ils se fondent sur la théorie des probabilités. Celle-ci encadre toutes les étapes de la production statistique : sélection de l’échantillon au sein de la population, ce qui suppose de disposer d’une base de données donnant une vue exhaustive de cette population ; traitement des réponses et correction de la non-réponse ; redressements ; calcul des intervalles de confiance, qui permettent de préciser le caractère interprétable des chiffres obtenus. Au total, une activité qui réclame une maîtrise autant théorique que pratique.
La statistique publique a pour but d’éclairer les faits économiques et sociaux du pays. Connaître la population ou les entreprises dans toutes les dimensions utiles à l’action publique est donc au cœur du métier de statisticien public. Pour cela, ce dernier dispose de bases de données administratives (bases fiscales, déclarations de données sociales, etc.). Il dispose aussi de l’enquête de recensement, réalisée tous les ans auprès de 15 % de la population française, mais avec un questionnaire réduit aux questions démographiques, d’activité et de logement. Ces éléments ne suffisent pas à connaître, par exemple, les conditions de vie des ménages ou les conditions d’insertion dans l’emploi et leurs évolutions au cours du temps. Il faut pour cela procéder à des enquêtes dédiées.
Extrapolation et cadre probabiliste
Ces enquêtes sont, depuis les années 1950, un outil majeur de la statistique publique. Elles constituent un moyen efficace de disposer d’informations précises permettant d’analyser les phénomènes sociaux-économiques, de comprendre les mécanismes individuels à l’œuvre et d’affiner les politiques publiques en conséquence. Les enquêtes sont donc des opérations auxquelles la statistique publique consacre beaucoup de soin et d’énergie afin de garantir la pertinence des analyses qui seront réalisées sur les données collectées.
Elles consistent à interroger non pas toute la population mais un échantillon de plusieurs milliers ou dizaines de milliers d’individus, ménages ou entreprises, et à extrapoler les données collectées via un questionnaire pour produire des résultats portant sur l’ensemble de la population concernée. Cette extrapolation est la pratique usuelle des enquêtes par sondage, quelles qu’elles soient. Les résultats obtenus in fine sont donc issus, après traitements, des déclarations des enquêtés.
Les enquêtes de la statistique publique se distinguent de la majeure partie des enquêtes d’autres organismes par le fait qu’elles s’inscrivent entièrement dans le cadre du calcul des probabilités, depuis la sélection des individus dans l’échantillon d’enquête jusqu’à la production des résultats et au calcul d’intervalles de confiance qui encadrent les grandeurs estimées définies sur la population générale. De cette spécificité découle la qualité des résultats tirés des données issues de l’échantillon.
Dans ce qui suit, nous passons en revue les différentes étapes de production statistique et d’analyse que permet l’inscription de l’enquête dans ce cadre probabiliste cohérent. Nous illustrons le cheminement d’analyse du statisticien d’enquête public à travers l’exemple de l’enquête Emploi en continu de l’Insee, récemment rénovée.
Bien définir le champ et les paramètres d’intérêt de l’enquête
Les données qui sont collectées puis traitées lors d’une enquête sont relatives à des individus, au sens large du terme (personnes physiques, entreprises, biens et services…). Lorsqu’ils sont considérés dans leur ensemble, les individus forment une population. Le statisticien a pour objectif premier de résumer une information complexe caractérisant une population. Pour cela, il va mesurer des grandeurs numériques sur cette population en agrégeant des données individuelles. Ces grandeurs, appelées paramètres d’intérêt, traduisent des concepts plus ou moins complexes : âge moyen, taux de chômage, valeur ajoutée moyenne par emploi, proportion de ménages ayant une voiture… Le plus souvent, elles s’expriment formellement par des totaux, des moyennes ou des proportions.
Dans un processus d’enquête, il convient en premier lieu de bien préciser le périmètre de la population, appelé champ de l’enquête. Il est naturellement défini à partir des paramètres d’intérêt jugés les plus importants, qu’il convient également d’expliciter. Une définition floue du champ et/ou des paramètres sera source d’erreur.
Par exemple, dans le cas de l’enquête Emploi, les paramètres d’intérêt principaux sont le taux d’emploi et le taux de chômage au sens du Bureau international du travail (BIT) parmi les résidents habituels sur le territoire français. Ces indicateurs sur le marché de l’emploi sont définis au niveau international et permettent une comparaison dans le temps et entre pays. Ces indicateurs sont par exemple différents du statut spontané déclaré par les personnes sur leur situation vis-à-vis du marché du travail, également recueilli dans l’enquête. Ainsi, en moyenne, en 2021, 7,9 % des personnes actives résidant en France (hors Mayotte) sont au chômage au sens du BIT alors qu’elles sont 12 % à se déclarer spontanément au chômage dans l’enquête. De même, le nombre de chômeurs au sens du BIT diffère du nombre de demandeurs d’emploi inscrits à Pôle Emploi. Tout résultat doit être relié au concept qu’on mesure, et également à son champ. L’enquête Emploi interroge les personnes résidant en France âgées de 15 à 89 ans et vivant en logements ordinaires, formant ainsi le champ de l’enquête (hors communautés comme des cités universitaires, des foyers de jeunes travailleurs, des casernes, des EHPAD, etc., les conditions pour une collecte de qualité dans ces populations spécifiques n’étant pas réunies). Au vu de la thématique de l’enquête, on estime qu’il n’est pas utile d’interroger les personnes en dehors de cette tranche d’âge puisque ces populations sont quasi exclusivement inactives.
Échantillonner pour réduire les coûts, au prix d’une erreur
Une collecte complète auprès d’une population de grande taille, comme la population des personnes résidant en France ou celle des entreprises, génère des coûts considérables. Pour contourner cet obstacle majeur, les statisticiens ont développé des méthodes d’enquête par sondage, consistant à effectuer une collecte sur une partie seulement de la population, appelée échantillon. On gagne ainsi en termes budgétaires, en rapidité de mise en œuvre et généralement aussi en qualité de collecte des données individuelles, grâce à la mobilisation d’un réseau d’enquêteurs bien formés, pour ce qui concerne du moins les enquêtes auprès des personnes physiques.
À l’exception de rares situations, les échantillons ont une composition aléatoire, c’est-à-dire que le hasard intervient dans leur constitution. En conséquence, et en contrepartie des gains évoqués ci-dessus, il faut accepter une erreur spécifique au sondage appelée erreur d’échantillonnage. En effet, puisque l’information dont on dispose ne concerne que l’échantillon, on ne peut pas prétendre mesurer exactement des paramètres définis sur le champ de l’enquête : il y a une différence numérique entre ce que l’on cherche à mesurer et ce que l’on calcule. Le statisticien doit donc se contenter d’une estimation de ces paramètres.
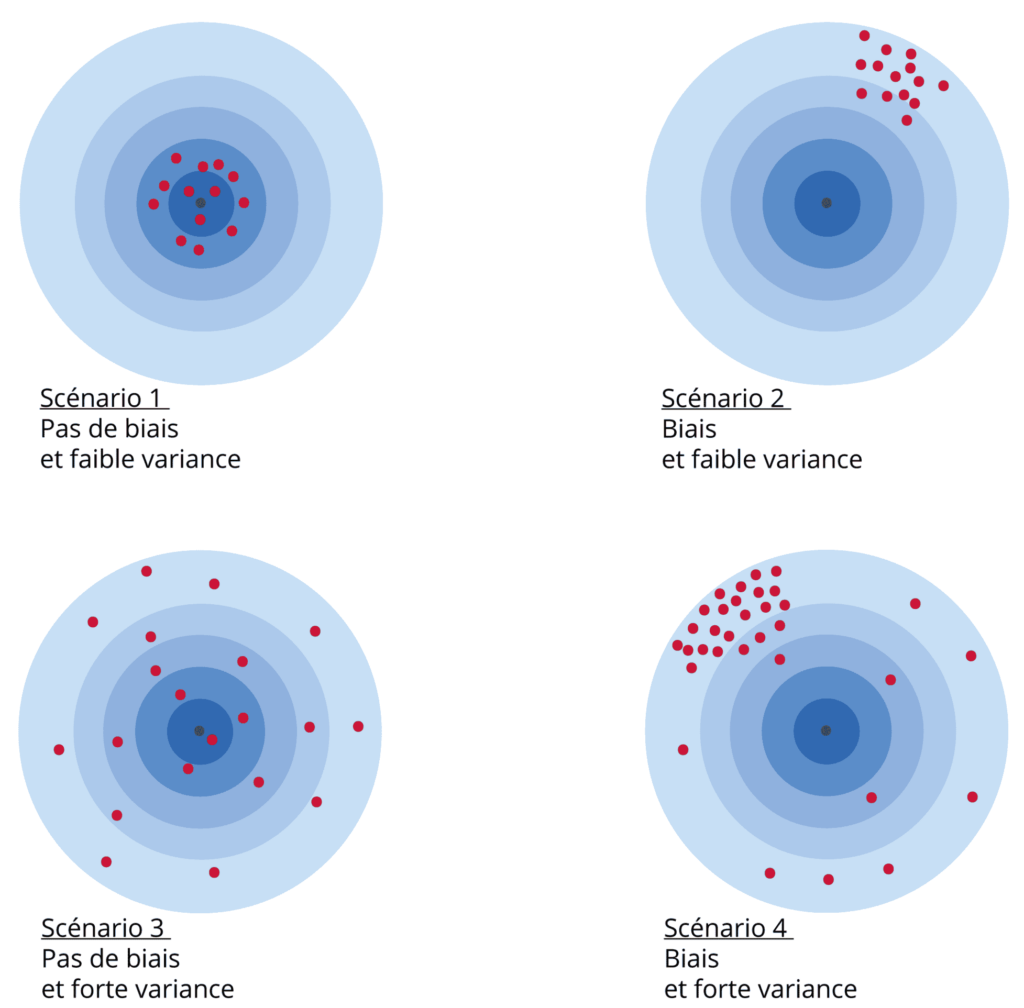
La théorie statistique conduit à apprécier cette erreur en moyenne au travers de deux concepts, que sont respectivement le biais et la variance d’échantillonnage. Supposons qu’en appliquant une méthode d’échantillonnage donnée, on tire successivement et de manière indépendante un grand nombre d’échantillons, et que l’on calcule la moyenne des différentes estimations associées aux différents échantillons obtenus : l’écart numérique entre cette moyenne et le paramètre d’intérêt s’appelle le biais d’échantillonnage. On peut définir un second indicateur qui mesure la variabilité de l’estimation associée à l’échantillon autour de sa moyenne. Il s’agit de la variance d’échantillonnage, qui est d’autant plus grande que l’on a de risque de produire des estimations éloignées numériquement de leur moyenne. On peut illustrer simplement le biais et la variance avec l’exemple suivant (figure 1) : lorsqu’on lance des fléchettes sur une cible, les impacts des fléchettes sont en partie guidés par le hasard. Si les différentes fléchettes lancées entourent harmonieusement le centre de la cible, on est en présence d’un tir « sans biais ». Si les fléchettes sont majoritairement positionnées en haut à droite de la cible (par exemple), il y a un biais. Par ailleurs, si le tir est groupé, c’est-à-dire si les fléchettes sont presque toutes localisées à proximité d’un même point de la cible, on sera en présence d’une faible variance. Si au contraire on trouve des fléchettes dispersées un peu partout sur la cible, la variance sera forte. Un objectif majeur du statisticien d’enquête est bien évidemment de produire une estimation avec un biais et une variance d’échantillonnage les plus faibles possibles.
Figure 1 – Biais et variance
Une base de sondage est indispensable pour échapper au biais
Les échantillonnages de la statistique publique sont produits à partir de systèmes d’information appelés bases de sondage. En pratique, il s’agit de fichiers listant tous les individus de la population constituant le champ de l’enquête, avec l’information nécessaire et suffisante pour pouvoir les repérer et les contacter (par exemple un nom, un prénom et une adresse, ou un numéro de téléphone, pour une personne physique). Les bases de sondage contiennent (presque) toujours d’autres informations caractérisant les individus. Ainsi, pour les enquêtes auprès des ménages et des personnes physiques, l’Insee mobilise actuellement une base de sondage nommée Fichier démographique des logements et des individus (Fidéli), fondée sur des sources de données fiscales. Cette base contient une information individuelle riche sur les revenus, ainsi que sur certaines caractéristiques sociodémographiques des ménages et des individus (âge, sexe, nombre de personnes dans le ménage…).
Le tirage d’un échantillon dans une base de sondage, tel que le pratique la statistique publique, permet de sélectionner l’échantillon en respectant une probabilité de tirage choisie au préalable. De ce fait, on bénéficie de deux propriétés essentielles : d’une part on peut former des estimations sans biais d’échantillonnage, d’autre part on peut réduire la variance d’échantillonnage. En particulier, on peut faire en sorte que chaque individu du champ ait une probabilité non nulle d’être échantillonné, faute de quoi l’estimation obtenue est biaisée. Ce sont des arguments centraux et majeurs pour obtenir la plus grande qualité possible à taille d’échantillon donnée. Lorsqu’on contrôle les probabilités de sélectionner les différents échantillons potentiellement sélectionnables, on est en mesure de mettre en œuvre des techniques d’échantillonnage plus efficaces en mobilisant l’information disponible dans la base de sondage. Parmi d’autres, une méthode puissante et moderne est celle de l’échantillonnage équilibré qui, tout en garantissant la sélection « au hasard » des individus, permet d’assurer que certaines grandeurs soient estimées de manière exacte, sans erreur d’échantillonnage. Dans l’enquête Emploi, on fait ainsi en sorte de tirer des logements dans une zone (appelée secteur) tels que, par exemple, les pourcentages de population par sexe et âge ou encore les revenus moyens des habitants de l’échantillon sélectionné soient égaux à ceux de la population de cette zone, connus à partir de la base de sondage.
L’imperfection des bases de sondage contribue à l’erreur d’estimation. Le risque le plus redouté est celui du défaut de couverture, qui survient lorsqu’une partie de la population n’est pas présente dans la base de sondage alors qu’elle participe à la définition du paramètre d’intérêt. Les individus de cette partie manquante de la population ont une probabilité nulle d’être sélectionnés dans l’échantillon, ce qui, comme on l’a vu, cause un biais. Ce serait le cas dans l’enquête Emploi, par exemple, des personnes sans abri si celles-ci étaient comptées dans le champ de l’enquête. En effet, s’agissant d’une sous-population par nature très difficile à localiser, il n’existe aucune base de sondage capable de produire, de manière régulière et avec une qualité correcte, un échantillon de personnes sans-abri. Pour ce qui concerne les personnes physiques vivant en ménage dit ordinaire, il apparaît que les bases de sondage utilisées par la statistique publique sont de très bonne qualité.
Une des manières (mais il y en a d’autres) de produire des échantillons en l’absence de base de sondage consiste à opter pour une approche dite empirique. Il s’agit le plus souvent d’effectuer une sélection simple et rapide de l’échantillon sur le terrain, relativement peu coûteuse. La contrepartie est une absence de maîtrise du cadre probabiliste de l’échantillonnage. Ces méthodes recouvrent essentiellement les enquêtes « par quotas », les échantillonnages auprès de volontaires, et les sélections d’unités-type. Les enquêtes par quotas ont pour principe de produire des échantillons ayant la même structure que la population du champ selon certaines variables – par exemple on impose la même structure par sexe et la même structure par tranche d’âge – mais les unités sont échantillonnées sur le terrain par les enquêteurs en fonction de consignes générales ayant pour objectif « d’aléatoiriser » au maximum la sélection. Ces méthodes, historiquement les premières mises en œuvre, sont susceptibles de produire des biais d’échantillonnage potentiellement significatifs : c’est pourquoi l’Insee ne les utilise pas et s’en tient aux méthodes probabilistes. En effet, le risque essentiel encouru est celui d’un mécanisme pernicieux qui conduirait les enquêteurs à sélectionner les individus en relation – plus ou moins manifeste – avec l’information que l’on collecte, et on vérifie techniquement que ce type de liaison se traduit par du biais, en l’absence de maîtrise des probabilités de sélection des individus. Si on voulait effectuer une enquête Emploi par quotas en face-à-face par exemple, on risquerait d’interroger plus probablement des personnes plus faciles à trouver en journée à leur domicile ou dans un lieu public, donc moins souvent en emploi, ce qui conduirait à une sous-estimation en moyenne du paramètre « taux d’emploi ». En outre, il est très difficile, avec ce type de méthode, d’assurer que tous les individus ont une probabilité non nulle de participer à l’enquête. Les enquêtes auprès de volontaires, essentiellement effectuées par internet, subissent ce risque encore bien davantage et elles ne sont pour cette raison jamais pratiquées par l’Insee.
A contrario, l’inscription de l’enquête dans un cadre probabiliste avec sélection dans une base de sondage permet de maîtriser l’ordre de grandeur de l’écart entre échantillon sélectionné et vraie population. Ainsi, pour l’échantillon de l’enquête Emploi, l’écart relatif entre le nombre de chômeurs (individus percevant une allocation chômage) en France extrapolé à partir de l’échantillon sélectionné à l’ensemble de la population et le « vrai » nombre de chômeurs si on pouvait l’obtenir à partir de la base de sondage serait d’environ 0,1 %, d’après les évaluations réalisées lors du tirage de l’échantillon (voir « Le renouvellement de l’échantillon-maître des enquêtes auprès des ménages et de l’échantillon de l’enquête Emploi de l’Insee », p. 150).
Pondérer et corriger la sélection des répondants
Dans une enquête par sondage, le calcul des estimations repose fondamentalement sur un système de pondération (voir aussi figure 2 sur le processus d’estimation). Le principe de cette phase consiste à affecter à tout individu échantillonné un coefficient d’extrapolation pertinent, appelé poids de sondage, qui vient multiplier les valeurs des réponses qu’il a fournies. Les poids interviennent dans les expressions de toutes les estimations. Le poids est obtenu selon la théorie comme l’inverse de la probabilité de sélection et il s’interprète comme le nombre d’individus de la population que l’individu échantillonné représente.
La pondération dépend initialement de la méthode d’échantillonnage retenue. Souvent, les poids sont les mêmes pour tous les individus échantillonnés, mais parfois l’Insee opte pour une stratégie de surreprésentation de certaines catégories, qui consiste à donner plus de chances de sélectionner certains individus que d’autres, et cela conduit à utiliser in fine des poids différenciés.
Le poids conditionne la qualité de l’estimation, en particulier son biais et sa variance d’échantillonnage. Dans le cadre probabiliste qu’on s’est donné, on sait définir des poids théoriques pour obtenir des estimations sans biais. On sait également, pour chaque méthode d’échantillonnage, adapter les poids pour minimiser la variance d’échantillonnage. Cela est possible parce que, fondamentalement, la maîtrise probabiliste du processus de passage de la population à l’échantillon permet de réaliser « proprement » l’opération inverse que constitue l’extrapolation, qui est au cœur de la phase d’estimation. C’est aussi pourquoi ces propriétés n’ont pas d’équivalent dans les approches empiriques.
Au-delà de la théorie, la réalité du terrain apporte une première perturbation : la non-réponse. Inévitable en pratique, elle survient à chaque fois qu’on ne dispose pas de la donnée individuelle que l’on cherche à collecter. Les causes en sont multiples : individu impossible à localiser, individu impossible à joindre, refus de réponse, individu inapte à répondre, information collectée aberrante, etc. La non-réponse est assimilable en théorie à une phase supplémentaire de sélection – que le statisticien doit cette fois subir – qui augmente la variance des estimations et génère potentiellement du biais. Par exemple, dans l’enquête Emploi, 25 % des logements de l’échantillon n’ont pas répondu à l’enquête au premier trimestre 2021. On verra par la suite que cette non-réponse se traduit par une légère augmentation de la variance d’échantillonnage.
Figure 2 – Processus d’estimation
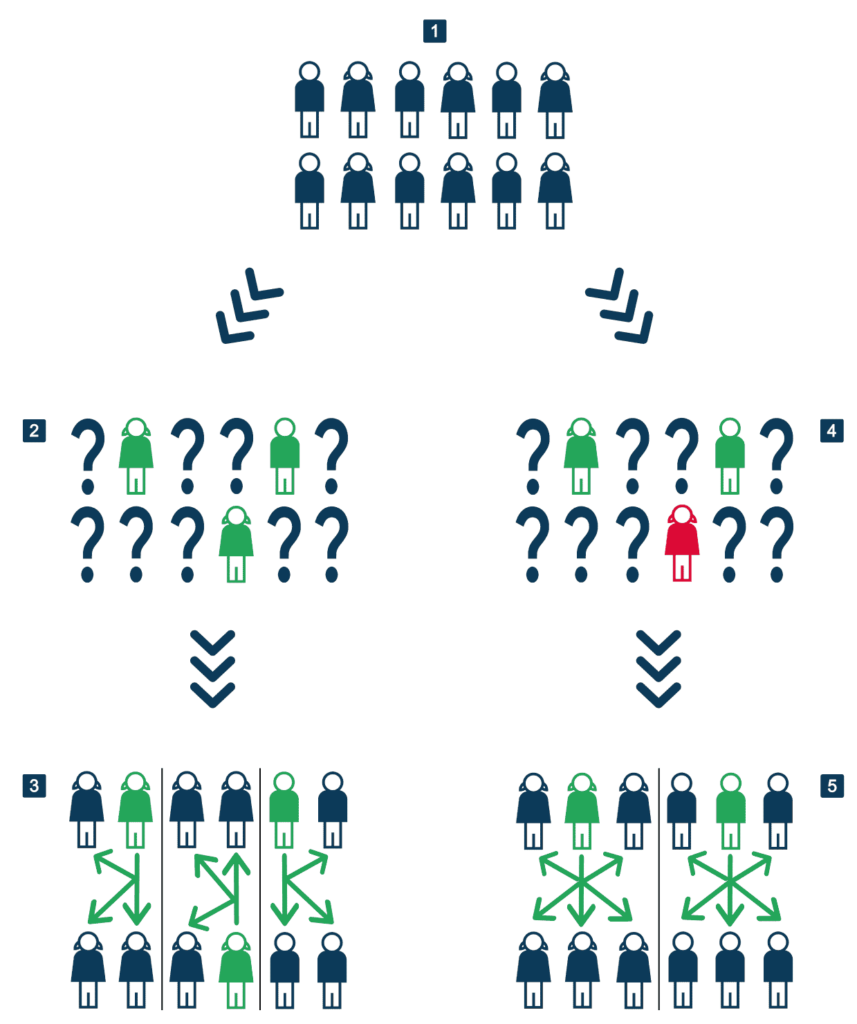
Lecture point 1 : soit une population de 12 personnes, composée à parts égales de femmes et d’hommes.
Lecture point 2 : on tire au hasard 3 personnes, qui représentent l’échantillon de la population de départ. Ce hasard désigne 2 femmes et 1 homme, et chacun répond à l’enquête.
Lecture point 3 : c’est le mécanisme d’inférence : chaque individu de l’échantillon est dupliqué 12/3 = 4 fois. Ici, l’estimation de la composition de la population totale est erronée puisqu’elle est censée être composée de 8 femmes et de 4 hommes.
Lecture point 4 : dans ce cas, une personne ne répond pas (et c’est une femme).
Lecture point 5 : on duplique comme au point 3, mais comme cette fois il y a 2 répondants, la duplication, ou le poids, est de 12/2 = 6. Par un heureux hasard, on retombe sur la répartition de la population de départ (imaginez le cas –désastreux – où le non-répondant serait l’homme…).
La première mesure arrêtée par la statistique publique est bien entendu de tout faire en amont pour limiter la non-réponse. Cela prend diverses formes : souci permanent de réduire la charge des enquêtés en limitant les sollicitations au cours du temps, formation approfondie des enquêteurs pour localiser et savoir convaincre les enquêtés de participer, proposition de modes de collectes alternatifs plus adaptés pour l’enquêté, etc.
Malgré ces efforts, l’enquête Emploi, comme toutes les enquêtes, est affectée d’une fraction de non-réponse qui déforme la structure de la population du champ de l’enquête (figure 3) : par exemple, les jeunes adultes (18-24 ans) ont tendance à moins répondre à l’enquête, tandis que les personnes âgées de 65 ans ou plus répondent davantage que la moyenne et sont donc sur-représentées parmi les répondants.
Figure 3 – Structure par âge dans la population du champ et parmi les répondants à l’enquête Emploi
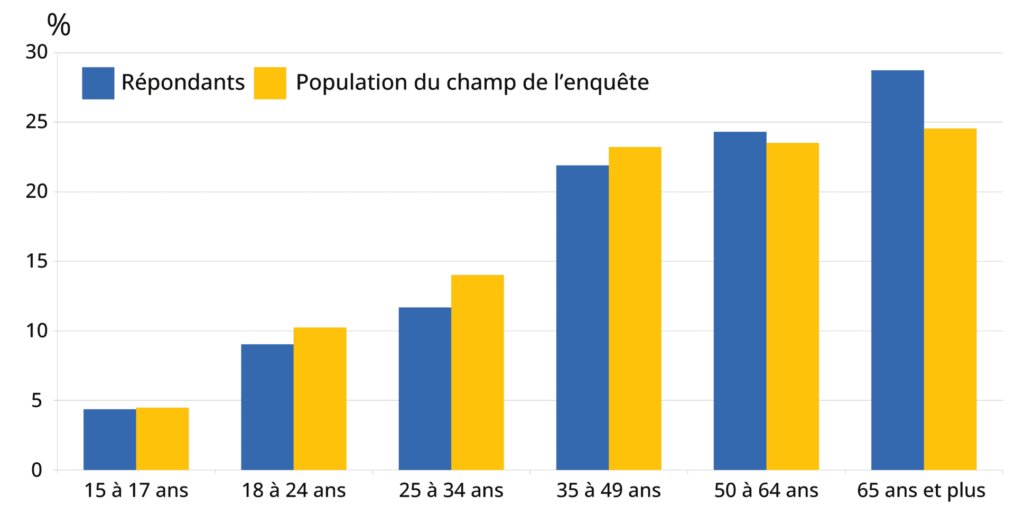
Source : Insee, enquête Emploi premier trimestre 2021.
Lorsque la non-réponse a été réduite au minimum, on applique, pour en limiter les effets, des traitements qui distinguent deux formes de non-réponse. Quand elle ne concerne que certaines questions – on parle de non-réponse partielle – la technique la plus utilisée pour la corriger consiste à prédire les valeurs individuelles manquantes. Quand la non-réponse affecte l’intégralité du questionnaire, on a affaire à une non-réponse dite totale. La technique de correction la plus utilisée consiste à agir sur la pondération des répondants afin qu’ils représentent les non-répondants. La méthode classique suppose que chaque individu de l’échantillon peut répondre – ou ne pas répondre – « au hasard », avec une certaine probabilité dont on postule l’expression et que l’on cherche à calculer. Cette probabilité relève d’un modèle : elle est estimée à partir des informations disponibles dans la base de sondage, par exemple l’âge pour corriger la déformation observée dans la figure 3. Malgré toutes les précautions que l’on peut prendre lors de cette modélisation, il y a toujours peu ou prou une relation résiduelle entre l’information que l’on collecte et la participation à l’enquête. Le statisticien a pour objectif de minimiser le biais qui en résulte en mobilisant l’information la plus pertinente, ce qui renforce l’importance de disposer d’une base de sondage la plus riche possible en informations. La probabilité de réponse estimée est ensuite intégrée à la pondération finale, au même titre que la probabilité de sélection. Grâce à cette méthodologie, on est en mesure de considérer la non-réponse comme une étape probabiliste, au même titre que l’échantillonnage initial.
La correction de non-réponse de l’enquête Emploi permet d’aligner la structure des répondants sur celle de la population du champ (figure 3). Cette correction de la structure socio-démographique peut alors avoir un impact sur l’estimation des paramètres d’intérêt de l’enquête. Par exemple, au premier trimestre de l’année 2021, le taux de chômage des seuls répondants est estimé à 7,7 % en métropole. Après correction de la non-réponse, il est estimé à 8,1 %.
Calculer des intervalles de confiance sur les statistiques produites
La théorie des sondages permet de calculer une variance d’échantillonnage, laquelle quantifie la sensibilité de l’estimation à la façon dont a été constitué l’échantillon, et prend aussi en compte la phase de non-réponse. Une grande variance signifie que l’estimation obtenue dépend beaucoup de l’échantillon tiré et répondant, ce qui entraîne une incertitude sur les résultats diffusés et traduit de fait une enquête de qualité médiocre.
De la variance, on tire un intervalle de confiance : plutôt qu’une estimation ponctuelle du paramètre d’intérêt, c’est un « encadrement » calculé de façon à contenir ce paramètre avec une très forte probabilité – souvent 95 chances sur 100. On parle communément de calcul de précision. Ainsi, dans l’enquête Emploi, au premier trimestre 2021, le taux de chômage en métropole est estimé à 8,1 %. L’intervalle de confiance à 95 %, centré sur cette valeur, s’établit à 8,1 % ± 0,3 %, soit un intervalle de [7,8 % ; 8,4 %]. Il y a donc 95 chances sur 100 pour que le « vrai » taux de chômage soit compris entre 7,8 % et 8,4 %. Pour revenir sur l’effet perturbateur de la non-réponse, on a pu vérifier qu’après tous les traitements statistiques visant à le limiter, la largeur de cet intervalle de confiance serait réduite de 3 % si l’intégralité de l’échantillon tiré était répondant.
L’intervalle de confiance n’est calculable que si l’estimation est sans biais. Pour cette raison, et parce que le calcul de variance nécessite la maîtrise des probabilités d’échantillonnage, l’intervalle de confiance ne peut être utilisé, en toute rigueur, que pour les enquêtes probabilistes. On peut montrer que sa largeur varie comme l’inverse de la racine carrée de la taille de l’échantillon répondant.
L’Insee, comme tous les producteurs d’enquêtes disposant d’une base de sondage, utilise l’information qu’elle contient pour réduire la largeur des intervalles de confiance. Dans cet objectif, des techniques dites de « redressement » ont été développées pour tirer profit des relations de corrélation existant entre ces informations et les données collectées par l’enquête. Les redressements mobilisent très souvent certaines informations fournies par des fichiers autres que la base de sondage, sous condition qu’ils couvrent l’intégralité du champ de l’enquête. Les gains de précision permis par les redressements sont souvent importants. Dans le même temps, l’Insee bénéficie de redressements très performants car il dispose de nombreux fichiers contenant une information riche, bien explicative de la plupart des phénomènes étudiés dans ses enquêtes : par exemple on va exploiter le fait de résider ou non dans un quartier de la politique de la ville (QPV), ainsi que le montant du revenu d’activité, pour améliorer l’estimation du taux de chômage.
Produire des statistiques en toute transparence sur les méthodes utilisées
L’Insee assure une large transparence des méthodes statistiques qu’il utilise pour traiter les données d’enquête et produire les estimations diffusées. Le site insee.fr fournit une information méthodologique accessible et synthétique, les compléments plus techniques figurent dans la documentation scientifique publiée dans les revues spécialisées et les colloques scientifiques. Des outils d’échantillonnage et de redressement bien documentés sont mis gratuitement à disposition des utilisateurs sur le site insee.fr.
Et, dans le but d’assurer un regard extérieur à l’Insee sur la qualité et les procédures d’enquête, un Comité du Label a été créé par le législateur. Ce comité examine la conformité des pratiques à l’état de l’art pour chaque enquête et propose, le cas échéant, leur labellisation d’intérêt général et de qualité statistique, l’enquête faisant alors l’objet d’une inscription au programme annuel d’enquêtes publié au journal officiel.
GLOSSAIRE – HUIT MOTS-CLÉS DES SONDAGES
Champ de l’enquête : ensemble des individus qui sont concernés par l’étude. Par exemple, interroger des enfants de moins de 15 ans n’a pas d’intérêt pour une étude sur l’emploi et le chômage.
Paramètre d’intérêt : grandeur numérique définie dans le champ de l’enquête et en lien avec l’étude, que l’on cherche à estimer. Exemples : âge moyen, taux de chômage, valeur ajoutée moyenne par emploi, proportion de ménages ayant une voiture…
Base de sondage : fichier constitué par l’ensemble des individus dans lequel on va tirer l’échantillon, coïncidant idéalement avec le champ de l’enquête. La base doit contenir au minimum des informations permettant d’identifier et de contacter les individus (ménages, personnes ou entreprises), comme le nom ou la raison sociale et l’adresse. L’enquête vise à récolter des informations individuelles que la base ne contient pas. Une base de sondage de personnes physiques peut être par exemple constituée par l’ensemble des individus recensés une année donnée sur un territoire donné.
Défaut de couverture : il survient lorsqu’une partie de la population n’est pas présente dans la base de sondage alors qu’elle est dans le champ de l’enquête et participe à la définition du paramètre d’intérêt.
Échantillon : sous-partie de la population formant le champ de l’enquête et sélectionnée pour être interrogée. La statistique publique procède par tirage au hasard dans une base de sondage des individus qui vont constituer l’échantillon.
Biais et variance d’échantillonnage : l’erreur moyenne liée au fait d’interroger un échantillon plutôt que la totalité de la population s’apprécie au travers de deux concepts, le biais et la variance. Supposons qu’en appliquant une méthode d’échantillonnage donnée, on tire successivement et de manière indépendante un grand nombre d’échantillons, et que l’on calcule la moyenne des différentes estimations associées aux différents échantillons obtenus (Me) : l’écart numérique entre cette moyenne et le paramètre d’intérêt s’appelle le biais d’échantillonnage. L’indicateur qui mesure la variabilité des estimations associées aux différents échantillons autour de leur moyenne (Me) est la variance d’échantillonnage.
Intervalle de confiance : « encadrement » calculé de façon à contenir le paramètre d’intérêt avec une très forte probabilité – souvent 95 chances sur 100. On parle communément de calcul de précision. L’intervalle ne peut être déterminé que lorsque l’échantillon est tiré dans un cadre probabiliste. ■
Pour en savoir plus
- Ardilly P., Les techniques de sondage, Éditions Technip, 2006
- Ardilly P., Lavallée P., Les sondages pas à pas, Éditions Technip, 2017
- Chevalier M. et al. 2022, « Le renouvellement de l’échantillon-maître des enquêtes auprès des ménages et de l’échantillon de l’enquête Emploi de l’Insee », Insee Méthodes n° 141, 2022
- Deville J.-C., 2006, Peut-on croire aux sondages ?, Pour la science n° 344, juin 2006
- Droesbeke J.-J., Vermandele C., Ce que nous disent les sondages, Académie royale de Belgique, Collection L’Académie en poche, 2019
- Guillaumat-Taillé F., Tavan C., « Une nouvelle enquête Emploi en 2021 : entre impératif européen et volonté de modernisation », Courrier des Statistiques n° 6, 2021
- Sillard P., Faivre S., Paliod N., Vincent L., « Pour les enquêtes auprès des ménages, l’Insee rénove ses échantillons », Courrier des Statistiques n° 4, 2020
- Tillé Y., Théorie des sondages, Éditions Dunod, 2019
Crédits photo : © LChevret





