Données sur les Quartiers prioritaires de la politique de la ville (QPV) : une nouvelle méthode pour protéger le secret statistique
L’actualisation de la géographie des Quartiers prioritaires de la politique de la ville (QPV) en 2024 soulève une difficulté pour l’Insee : diffuser des informations statistiques relatives aux anciens et nouveaux QPV, tout en protégeant le secret statistique. La proximité entre les contours des anciens et des nouveaux quartiers peut en effet conduire à des risques de rupture du secret par « différenciation géographique » sur certaines zones.
La solution traditionnelle de « masquer » des cases dans les fichiers de données diffusés atteint ses limites : elle conduit à supprimer un très grand nombre de cases et la perte d’information est trop importante.
Afin de dépasser ces limites, l’Insee mobilise désormais une nouvelle méthode de gestion de la confidentialité, dite des « clés aléatoires » (cell key method). Au lieu de masquer des cases, cette méthode consiste à « bruiter » légèrement les données d’origine avec une perturbation aléatoire, qui doit à la fois être suffisante pour garantir le secret et pas trop grande pour minimiser la perte d’information.
Afin d’éclairer le débat public sur la politique de la ville, l’Insee publie régulièrement des fichiers de données statistiques sur les Quartiers prioritaires de la politique de la ville (QPV), qui permettent aux acteurs intéressés d’étudier les caractéristiques des populations qui habitent ces quartiers. Il s’agit entre autres des estimations démographiques à partir du recensement de la population, des indicateurs de niveau de vie et d’inégalités ou du nombre de demandeurs d’emploi. Avant publication, ces fichiers de données font l’objet d’un traitement afin de protéger le secret statistique, c’est-à-dire rendre impossible l’identification et la divulgation de la situation d’une personne en particulier à partir des données diffusées.
La géographie prioritaire a été actualisée : les contours des QPV de France métropolitaine ont été revus au 1er janvier 2024 afin de prendre en compte les évolutions démographiques et économiques des territoires depuis la mise en place des QPV en 2015. Cette opération, réalisée par l’Agence nationale de la cohésion des territoires et les préfectures de département, s’est appuyée sur les données du Fichier localisé social et fiscal (Filosofi) de l’Insee. L’Insee a proposé un portrait statistique de ces nouveaux QPV en août 2024. Les QPV des départements et territoires d’outre-mer ont eux été actualisés le 1er janvier 2025 à partir des données du recensement de la population.
Suite à cette actualisation, l’Insee publie désormais des fichiers de données conjointement sur l’ancien zonage en QPV (dit « QPV 2015 ») et sur le nouveau (« QPV 2024 »). La poursuite de la publication en QPV 2015 est une demande forte des acteurs de la politique de la ville, afin en particulier de pouvoir suivre dans le temps long des quartiers qui sont sortis de la géographie prioritaire en 2024.
Le recoupement entre les deux zonages conduit à une augmentation des risques de rupture du secret statistique : quand deux zones sont proches sans être parfaitement identiques, il peut être facile de déduire des éléments sur la différence entre ces deux zones à partir des seules statistiques agrégées diffusées (on parle alors de « différenciation géographique »). Ce billet de blog revient sur cet accroissement du risque de rupture du secret statistique et présente la nouvelle méthode utilisée par l’Insee pour garantir le secret des données diffusées sur les QPV. L’Institut étudie l’application de méthodes du même type à d’autres cas d’usage à l’avenir.
Garantir le secret statistique : une obligation constante
La protection du secret statistique est inscrite dans la loi de 1951 sur l’obligation, la coordination et le secret en matière de statistiques. Pour une source donnée, des règles de diffusion garantissent qu’aucune information portant sur moins de « x » personnes, ménages ou entreprises n’est révélée. Ce seuil de diffusion « x » est fixé par le producteur des données, par exemple à 11 ménages pour les données d’imposition des ménages ou à 5 individus pour les informations relatives aux demandeurs d’emploi. Ces règles prévalent à la fois pour la révélation directe d’information (secret primaire) mais également en cas de révélation indirecte (secret secondaire). Dans ce deuxième cas, il s’agit typiquement de ne pas permettre la reconstitution d’une composante par différence entre le total et la somme des autres composantes : par exemple, à partir du nombre total de demandeurs d’emploi et du nombre de demandeurs d’emploi de 26 ans et plus, il est possible de déterminer le nombre de demandeurs d’emploi de moins de 26 ans.
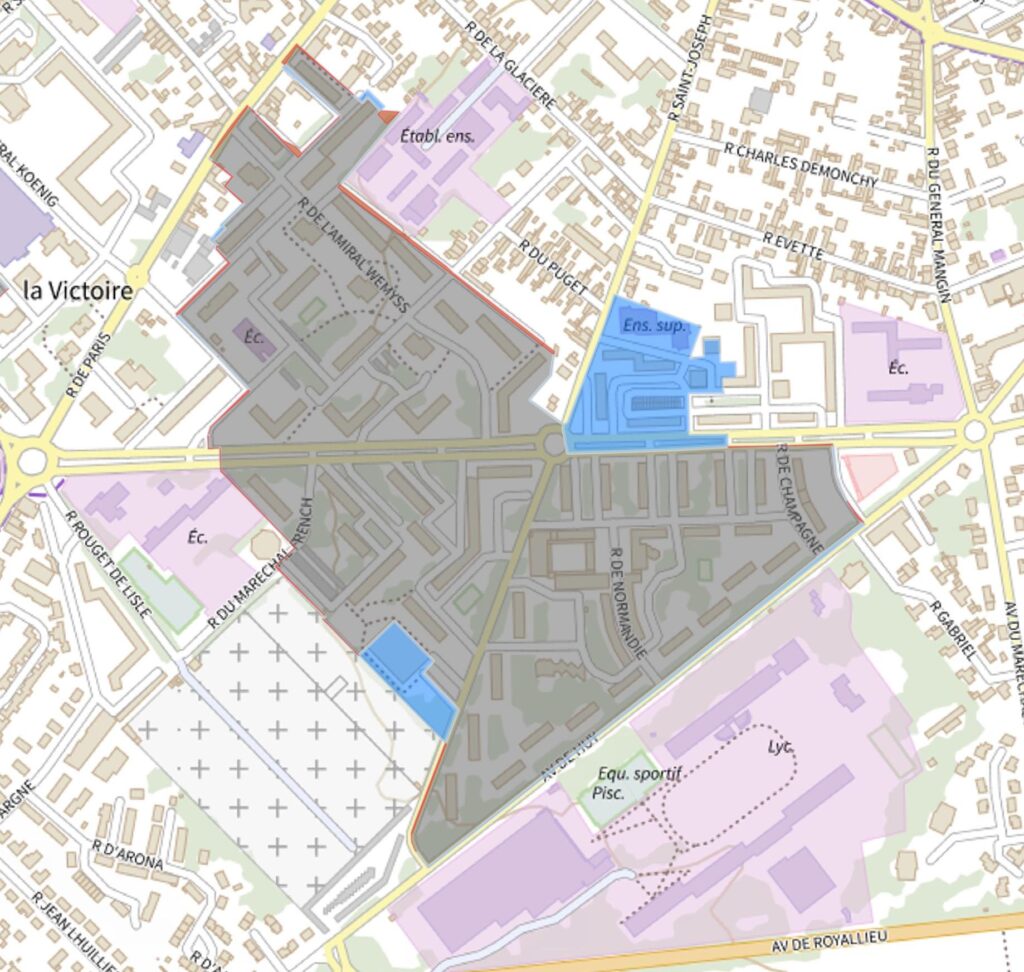
La diffusion de statistiques à des échelons géographiques fins et multiples ajoute une difficulté supplémentaire quant à la préservation du secret statistique. Afin de toujours mieux répondre aux besoins des acteurs locaux comme nationaux, l’Insee diffuse l’information statistique sur un ensemble grandissant de zonages dits « infra-communaux » : Îlots regroupés pour l’information statistique (IRIS), QPV voire carreaux de 200 m de côté. Or le risque de divulgation est accru dans le cas d’une diffusion statistique sur des territoires géographiquement proches. Par « différenciation géographique », il est en effet possible, à partir d’indicateurs additifs (par exemple le nombre de ménages sous le seuil de pauvreté), de déduire les caractéristiques de la population résidant dans le territoire correspondant à la différence géographique de deux territoires proches. C’est ce que montre la figure 1 sur un exemple à Compiègne : le quartier prioritaire La Victoire a été légèrement étendu (parties bleues) lors de l’actualisation au 1er janvier 2024. La diffusion simultanée de statistiques sur l’ancien périmètre (en gris) et le nouveau (partie grise et bleue) permet en l’absence de mesure de protection de révéler les caractéristiques de la population dans la zone bleue par différence.
Figure 1 – Exemple de risque de différenciation géographique à Compiègne
La solution de masquer des cases atteint ses limites
La méthode traditionnellement appliquée à l’Insee pour protéger le secret statistique est « suppressive » : la valeur des cases d’un tableau de données faisant courir un risque de rupture du secret est remplacée par une « valeur manquante », c’est-à-dire que la valeur initiale est tout simplement effacée du fichier (on parle de ce fait de « blanchiment » des cases). De plus, afin que l’information masquée ne puisse pas être reconstituée, d’autres suppressions en cascade peuvent alors être nécessaires au titre du secret secondaire ou de la différenciation géographique que l’on vient d’évoquer.
Cette méthode suppressive peut conduire à masquer un nombre élevé de cases et la perte d’information peut alors être non négligeable. À titre d’illustration, pour la diffusion des statistiques des demandeurs d’emploi en 2021 à l’échelle des quartiers de la politique de la ville, le traitement du secret statistique a nécessité de blanchir plus de 3 000 cases du tableau de données sur environ 70 000 cases, soit une perte globale d’information de l’ordre de 5 %. Pour des caractéristiques fines ou rares de la population, le taux de suppression peut être bien plus élevé. De plus, la présence de cases « blanchies » au niveau QPV empêche l’agrégation par l’utilisateur des données à des niveaux géographiques supérieurs, par exemple l’ensemble des QPV d’un même Établissement public de coopération intercommunale (EPCI), qui est l’échelon administratif de référence pour la mise en œuvre de la politique de ville.
Enfin, en termes d’implémentation, la méthode usuelle de blanchiment soulève plusieurs difficultés techniques. En particulier, la détection des cases à blanchir au titre du secret secondaire et de la différenciation géographique peut s’avérer particulièrement complexe, notamment quand la diffusion est réalisée sur plusieurs échelons géographiques qui ne sont pas emboîtés les uns dans les autres, comme les IRIS, les QPV ou les carreaux de 200 m de côté.
Les méthodes « perturbatrices », une manière différente d’aborder le compromis protection-utilité
Afin de dépasser ces limites, l’Insee mobilise désormais une nouvelle famille de méthodes de protection du secret statistique, méthodes dites « perturbatrices » : au lieu de blanchir certaines cases, ces méthodes « bruitent » légèrement les données d’origine, c’est-à-dire modifient légèrement la valeur de certaines d’entre elles (voire toutes) avec une (petite) perturbation aléatoire.
Comme les méthodes de blanchiment, le choix d’une méthode perturbatrice résulte d’un compromis entre protection et utilité des données : mais alors qu’avec les méthodes de blanchiment le résultat est binaire (garder la valeur exacte ou blanchir), les méthodes perturbatrices permettent d’affiner ce compromis en dégradant plus ou moins l’information contenue dans les données individuelles. Cette dégradation doit être suffisante pour garantir la protection des données tout en maximisant leur utilité pour le public (minimiser la perte d’information originale).
À noter qu’un avantage important des méthodes perturbatrices modifiant toutes les cases d’un tableau est la protection contre le risque de différenciation géographique : comme toutes les cases sont (légèrement) bruitées, il n’est plus possible en pratique de déterminer avec certitude les caractéristiques d’individus qui se trouveraient à l’intersection entre plusieurs zonages diffusés indépendamment. Par exemple, si toutes les statistiques sont diffusées à ±3 unités, le risque que l’intersection de deux zonages (ou plus) révèle une information certaine sur moins de 5 personnes devient faible.
Principe de la méthode des clés aléatoires (cell key method)
Spécifiquement, la nouvelle méthode mise en œuvre par l’Insee est celle des « clés aléatoires » (cell key method). Elle repose sur l’attribution au hasard d’une « clé » (concrètement, un nombre compris entre 0 et 1) à chaque individu (personne, ménage, entreprise, etc.). Cette attribution est réalisée une fois pour toutes : chaque individu garde ensuite toujours la même clé pour tous les traitements qui suivront. Au moment de diffuser un tableau de données, les clés individuelles sont combinées avec une « matrice de transition » pour déterminer, en fonction de la valeur d’origine (non perturbée), la déviation à appliquer pour obtenir la valeur perturbée qui sera diffusée. Cette méthode est présentée plus en détails dans une fiche méthodologique.
Explication par l’exemple figure 2 :
Les données sur les demandeurs d’emploi sont diffusées QPV par QPV et ventilées par sexe et tranche d’âge (moins de 26 ans, de 26 à moins de 50 ans, 50 ans et plus). Le seuil de confidentialité qui régit leur diffusion est de 5 : en appliquant la méthode de gestion du secret, on vise donc à limiter la possibilité pour un utilisateur des données de savoir avec certitude, à partir de l’information diffusée sur les demandeurs d’emploi par sexe et tranche d’âge, si une information concerne moins de 5 individus.
Dans l’exemple de la figure 2, qui correspond à un QPV fictif, il y a seulement 3 hommes demandeurs d’emploi de moins de 26 ans. La diffusion directe de cette information contreviendrait donc aux règles de diffusion de la source.
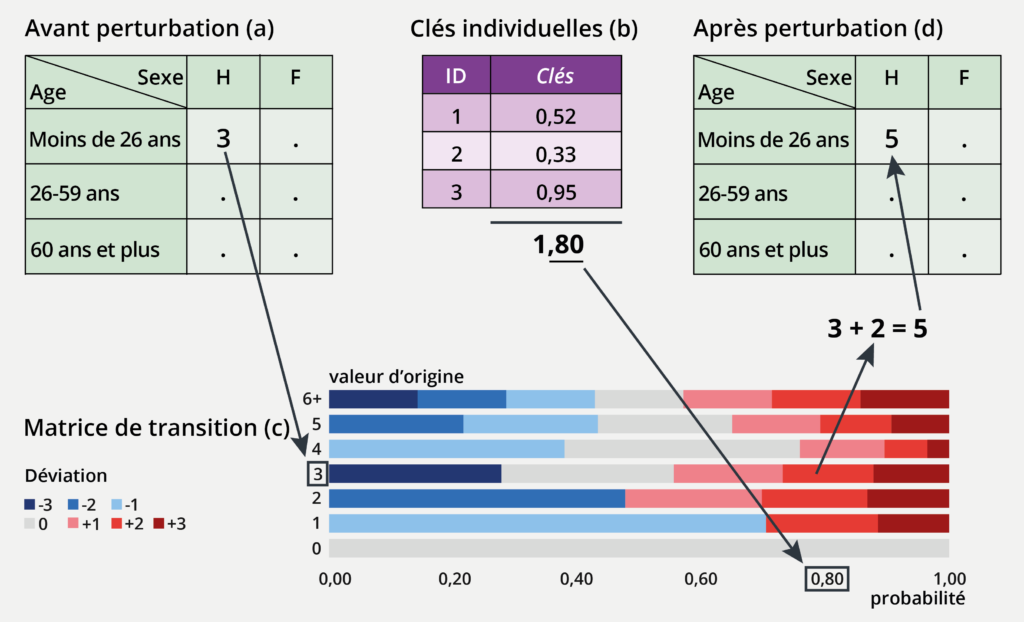
Figure 2 – Exemple d’application de la méthode des clés aléatoires
Dans ce cadre, la méthode des clés aléatoires est appliquée de la façon suivante :
1. Dans le fichier de données initial (non-perturbé) des demandeurs d’emploi, il y a 3 hommes de moins de 26 ans dans le QPV fictif (sous-figure a).
2. Chaque individu du fichier dispose d’une « clé individuelle » (un nombre compris entre 0 et 1) parfaitement aléatoire. C’est en particulier le cas pour les 3 hommes de moins de 26 ans de la case (sous-figure b).
3. Les clés individuelles des 3 hommes concernés sont sommées pour donner 1,80. Seules les décimales de cette somme seront utiles dans la suite, soit 0,80.
4. La valeur initiale (non-perturbée) détermine la ligne de la matrice de transition à utiliser (sous-figure c), ici celle correspondant à la valeur 3. Sur cette ligne, on se place au niveau de la partie décimale de la somme des clés calculée à l’étape précédente, soit 0,80.
5. La perturbation à appliquer à la valeur initiale est donnée par la valeur de la matrice de transition (sous-figure c) correspondante (ici +2).
6. La valeur perturbée est alors obtenue en appliquant la perturbation à la valeur initiale (ici 3 + 2 = 5).
7. Dans le fichier de données diffusé (sous-figure d), la valeur perturbée 5 vient remplacer la valeur initiale (non-perturbée) 3.
Cette méthode de perturbation présente de nombreuses propriétés intéressantes :
• bien que totalement aléatoire (en raison du caractère aléatoire des clés), elle garantit que c’est toujours la même perturbation qui est appliquée à un même comptage quel que soit le tableau de données dans lequel il apparaît. Cela est dû au fait que les clés individuelles sont fixées une fois pour toutes ;
• la matrice de transition respecte certaines contraintes, qui garantissent que les statistiques produites in fine n’induisent pas de biais systématique, ni à la baisse ni à la hausse. En d’autres termes, en appliquant cette méthode les statistiques sont perturbées aussi souvent à la baisse qu’à la hausse, si bien que les moyennes sont conservées. Cela garantit qu’en pratique, les conclusions tirées à partir de l’analyse des données perturbées seront similaires à celles qui auraient été tirées à partir des données non-perturbées ;
• le choix de la matrice de transition permet également de garantir – si on le souhaite – que les valeurs perturbées ne prendront jamais certaines valeurs. Dans l’exemple simplifié de la figure 2, il s’agit des valeurs 1 et 2 : aucune combinaison des valeurs initiales et des perturbations figurant dans la matrice ne peut conduire à ce que la valeur perturbée soit 1 ou 2 (par exemple, un 1 ne peut être perturbé qu’avec un -1, un +2 ou un +3, mais pas avec un 0 ou un +1).
La matrice réellement utilisée pour les données de demandeurs d’emploi est plus complexe et garantit qu’aucune donnée perturbée ne soit comprise entre 1 et 4. Les matrices de transition utilisées par l’Insee dans le cadre de la diffusion des QPV en 2025 garantissent toujours qu’aucune valeur perturbée ne sera inférieure au seuil de confidentialité de la source (5 pour les données de demandeurs d’emploi, 10 pour les données des bénéficiaires de l’assurance maladie, etc.). Si d’un point de vue théorique cette propriété n’est pas en elle-même absolument indispensable pour garantir un niveau de protection satisfaisant, elle y contribue néanmoins et rend par ailleurs plus tangible la protection apportée par la perturbation des données.
Quelques précautions d’usage mais une utilisation des données étendue et facilitée
Cette méthode appelle néanmoins quelques précautions nouvelles dans l’utilisation des données :
• la déviation maximale étant fixée, les petites valeurs sont relativement plus perturbées que les grandes : il est donc préférable de ne pas tirer de conclusions trop fortes d’analyses portant sur des tableaux dans lesquels la proportion de ces petites cases serait importante ;
• les décompositions d’un total selon les composantes sous-jacentes ne sont plus exactes. Par exemple, dans le fichier des demandeurs d’emploi, après perturbation le nombre total de demandeurs d’emploi ne coïncide en général pas avec la somme du nombre de demandeurs d’emploi ventilé par tranche d’âge (alors que c’est le cas dans les données non-perturbées). Cette « perte d’additivité » joue un rôle dans le mécanisme de protection du secret : si une méthode perturbatrice de protection du secret cherchait à garantir une cohérence parfaite entre un total et ses décompositions, alors la protection de certaines décompositions (de faibles effectifs en particulier) serait fragilisée.
À noter que pour garantir la protection des données diffusées sur différentes mailles géographiques contre le risque de différenciation, quand la méthode des clés aléatoires est utilisée pour la diffusion d’un fichier de données au niveau QPV (QPV 2015 et QPV 2024), elle l’est également pour la diffusion du même fichier au niveau IRIS.
* * * *
En conclusion, la diffusion de données protégées avec la méthode des clés aléatoires se fait en toute confiance :
• elle permet de protéger aussi bien du risque de rupture du secret que les méthodes suppressives tout en réduisant substantiellement les risques liés à la différenciation géographique : quand les données diffusées sont perturbées (même légèrement), il devient en pratique impossible de déduire des informations sur de petites zones obtenues par différence de deux zonages proches ;
• elle évite la suppression d’information et permet des opérations (agrégation en particulier) sur l’ensemble des tableaux : les données, bien que bruitées, ne sont pas statistiquement « fausses », c’est-à-dire que les analyses réalisées sur de tels tableaux, même poussées (tests d’indépendance, analyses factorielles, par exemple) conservent toute leur pertinence et ne conduisent pas les utilisateurs à conclure autrement que si elles avaient été menées sur les données non-perturbées ;
• elle réduit la complexité (et donc les risque d’erreurs) des traitements liés à la confidentialité. Elle facilite de ce fait la diffusion sur un plus grand nombre de zonages infra-communaux, car la diffusion sur un zonage n’est plus de nature à empêcher la diffusion sur un autre. ■
Pour en savoir plus
- Jamme J., 2025, « La méthode des clés aléatoires (cell key method) », Fiche méthodologique, janvier
- Insee, Données sur les quartiers 2024 de la politique de la ville, chiffres détaillés
- Insee, Données sur les quartiers 2015 de la politique de la ville, chiffres détaillés
- Cohen C., Potin-Finette A., 2024, « Portrait des nouveaux quartiers prioritaires de la politique de la ville en France métropolitaine », Insee Première n° 2008, août
Crédits photo : © «MysticaLink» – stock.adobe.com





